Research

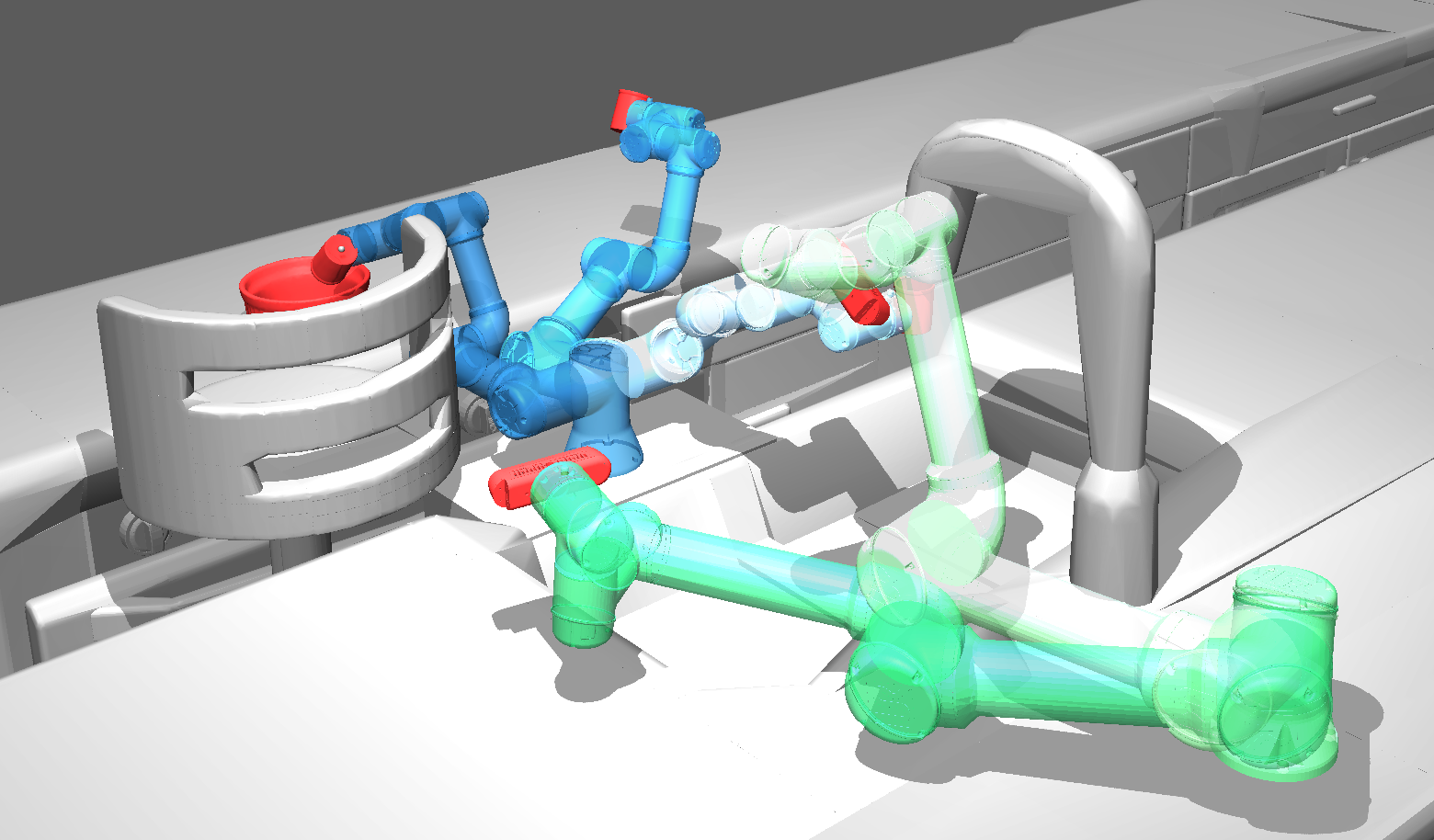
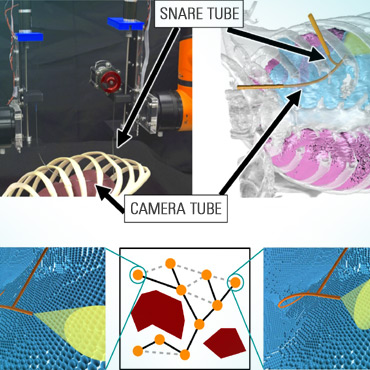
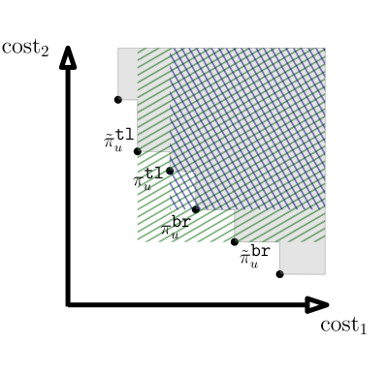
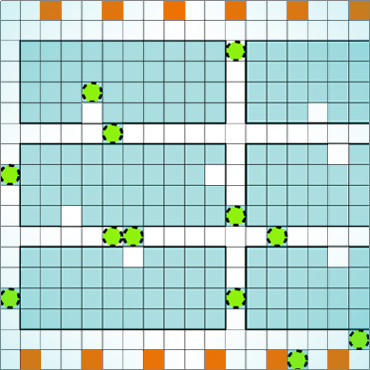
In the Computational Robotics Lab we seek to deeply understand and to rigorously address the computational challenges that arise when planning for robots. Our research, lying at the intersection of Computer Science and Robotics, is motivated by the key insight that in order to address these challenges, traditional Computer Science algorithms, tools and paradigms need to be revisited. This requires both (i) understanding and analyzing the unique domain-specific computational challenges in robotic planning and (ii) developing algorithms to address these challenges to provide the robotics community foundational tools to solve real-world problems.

A recent talk I gave at the UW robotics seminar describing the work we are doing on planning for continuum robots can be found here.

Task Assistance Planning

In task assistance planning, we are given two robots Rtask and Rassist. The first robot, Rtask, is in charge of performing a given task by executing a precomputed path. The second robot, Rassist, is in charge of assisting the task performed by Rtask using on-board sensors. The ability of Rassist to provide assistance to Rtask depends on the locations of both robots. Since Rtask is moving along its path, Rassist may also need to move to provide as much assistance as possible. The problem we study is how to compute a path for Rassist so as to maximize the portion of Rtask’s path for which assistance is provided.

more info

Even when we limit the problem to the setting where Rassist moves on a roadmap which is a graph embedded in its configuration space, this problem is NP-hard. Fortunately, we show that when Rassist moves on a given path, and all we have to do is compute the times at which Rassist should move from one configuration to the following one, we can solve the problem optimally in polynomial time. Together with carefully-crafted upper bounds, this polynomial-time algorithm is integrated into a Branch and Bound-based algorithm that can compute optimal solutions to the problem in an efficient manner. This problem has applications in diverse domains ranging from search-and-rescue to minimally-invasive robot surgey.

For a video visualizing our work click here.

For the algorithmic foundation of the problem including hardness results, click here.

Inspection Panning

From a minimally-invasive medical robot automatically inspecting the surface of a diseased organ to an autonomous quadcopter inspecting the structure of a bridge, robots in a variety of scenarios must plan their motions to efficiently inspect regions of interest. These are examples of robot-inspection planning tasks which arise in diverse applications. Here, we are tasked with planning motions for a robot that enable it to efficiently inspect a region of interest using its on-board sensors. Such an inspection plan should not only inspect the region of interest but also obey the robot's kinematic constraints, avoid obstacles (e.g., parts of a bridge or sensitive anatomical structures in bridge inspection and medical applications, respectively), and minimize some metric (such as time to completion or distance traveled), all while considering real-world uncertainties (e.g., uncertainty in the robot's kinematic model or external forces). Inspection planning is extremely challenging and naively-computed inspection plans may enable inspection of only a subset of the region of interest and may be highly suboptimal.

more info

Computing a high-quality inspection plan is important for many applications, e.g., a medical diagnostic inspection plan should minimize procedure duration to decrease the amount of time a patient is under anesthesia, all while thoroughly inspecting the region of interest. Current approaches to computing inspection plans are either highly tailored to specific applications, provide no guarantees on the quality of solution, or come with very long computation times for non-trivial problems, rendering them impractical for real-world applications.

Efficient Bi- and Multi-Objective Search Algorithms

The typical objective of search problems is to find a path between two nodes in a network such that some cost function is minimal on the chosen path, for example finding the shortest travel time between two locations on a street map. Search over large networks is a fundamental problem in computer science with numerous applications in the fields of robotics and artificial intelligence (AI). The larger the network, the more difficult it becomes to find these shortest paths. Furthermore, many applications are concerned with two (or more) competing resources, such as traversal time and energy consumption. Examples include solving transportation problems, planning power-transmission lines, scheduling satellites, and routing packets in computer networks. In these cases, there is a need for bi-objective (or multi-objective) search algorithms, where multiple-dimension cost functions are considered. To address this complicated problem, we combine ideas from existing bi-objective search algorithms with ideas from the AI search community to develop the next generation of optimal and approximately-optimal multi-objective search algorithms that will allow for real-time searches on much larger networks than possible using current techniques.

Multi-Agent Path Finding

Coordinating the movement of a fleet of agents or robots is a decades-old family of problems, which has been intensively studied by the robotics and AI communities with applications in diverse settings including assembly, evacuation, micro-droplet manipulation and search-and-rescue. One specific application is the logistics domain: Modern warehouses store inventory pods where a large number of robots autonomously pick up, carry and release the pods from their storage locations to designated dropooff locations where needed goods are manually removed from the pods (to be packaged and then shipped to customers). The successful use of robots in warehouses led to a multi-billion industry led by tech-giants such as Amazon robotics and Alibaba.

more info

We are interested in two types of problems that can be used to model such applications. In the first, called Multi Agent Path Finding (MAPF), the objective is to find collision-free paths for a given set of agents from their start to their goal locations. In the second, called multi-agent pickup and delivery (MAPD), agents have to attend to a stream of delivery tasks. Here, we need to assign each delivery task to an agent. This agent has to first move to the assigned pickup location and then to the assigned delivery location while avoiding collisions with the environment obstacles as well as with other agents.

For some of the open challenges in the field, check out our recent blue-sky paper published at AAMAS 20.