Ongoing Projects

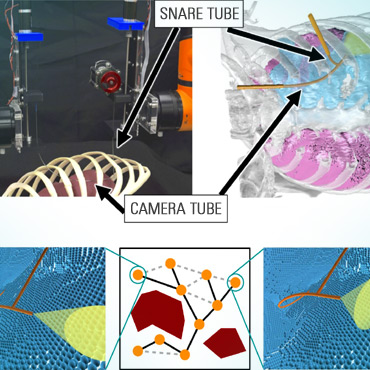
A great way to get hands-on experience with the field of algorithmic robot motion planning is to participate in a semester-long project (all while getting academic credit). These projects are aimed both for advanced undergraduate students as well as graduate students taking their first steps conducting research. Prospective students are expected to be hard working and independent. In contrast to class exercises, most of these projects contain some research element – this means that the solutions to some of the challenges posed are not clear upfront and creative solutions may be the basis of a Masters thesis.

Each project contains the prerequisite courses and a general description, typically with the relevant paper(s) mentioned. If you are interested in working on one of these projects please reach out to me with an email describing your background and the project(s) that you are interested in (if you want to suggest your own project – great!). Make sure you have the necessary background, carefully read the project description and relevant papers – this will allow us to have a meaningful and productive discussion when we meet.

Redundant Inspection Planning

Supervisor(s):Prof. Oren Salzman, Projects

Requirements:Advanced topics in robotics (236610)

From a minimally-invasive medical robot automatically inspecting the surface of a diseased organ to an autonomous quadcopter inspecting the structure of a bridge, robots in a variety of scenarios must plan their motions to efficiently inspect regions of interest. These are examples of robot-inspection planning tasks which arise in diverse applications. Here, we are tasked with planning motions for a robot that enable it to efficiently inspect a region of interest using its on-board sensors. Such an inspection plan should not only inspect the region of interest but also obey the robot's kinematic constraints, avoid obstacles (e.g., parts of a bridge or sensitive anatomical structures in bridge inspection and medical applications, respectively), and minimize some metric (such as time to completion or distance traveled). Inspection planning is extremely challenging and naively-computed inspection plans may enable inspection of only a subset of the region of interest and may be highly suboptimal.

more info

However, computing a high-quality inspection plan is important for many applications, e.g., a medical diagnostic inspection plan should minimize procedure duration to decrease the amount of time a patient is under anesthesia, all while thoroughly inspecting the region of interest. In this project we consider the problem of redundant inspection planning. Specifically, given a set of points of interest and some parameter k, we want to compute a path such that every point of interest is seen from at least k different configurations.

Additional details can be found here.

close

Multi-Agent Path Finding (MAPF): from Theory to Practice

Supervisor(s):Hadar Kaminsky

Requirements:Intro to AI (236501)

In this project, the student will learn and fully understand an algorithm called Conflict Based Search (CBS) . CBS is an algorithm that solves the MAPF problem and returns an optimal solution. In common CBS scenario, we assume that the agent (robot) is a point robot, meaning, it can either go up, down, right, or left without the need of turning. This assumption does not always hold in real-life, many robots can move to a direction only if they face it.

more info

In this project, the students will extend CBS algorithm to account not only for the location of the robot in each time step but also for its orientation. As a result at each time step, an agent can either move to a neighboring location, wait, or turn. This solution will produce a plan for a real-life scenario that vanilla CBS does not handle.

Additional details can be found here.

close

Multi-Objective Multi-Agent Path Finding (MAPF)

Supervisor(s):Prof. Oren Salzman

Requirements:Intro to AI (236501)

In this project we will explore the problem of computing solutions to the MAPF problem that balance between the makespan and the flowtime. This is a specific instance of a general family of problems called Bi-criteria optimization. Here we wish to compute all solutions where no solution is strictly better then the others for both cost functions, a set called the Pareto-optimal frontier. Additional details can be found here.

Time Efficient Curvature Constrained Planning

Supervisor(s):Prof. Oren Salzman

In this project, we are interested in computing curvature constrained paths for a robot moving amidst obstacles in the plane. Namely, we have a robot that has a minimum turning radius that it can follow. This constraint allows to model a wide range of systems such as UAVs and steerable needles and has attracted increasing attention in the planning community. Here, we are interested in a non-trivial cost function---minimizing travel time (and not path length). In many settings, taking longer manoeuvres at a higher speed is favorable (with respect to travel time) when compared to short, but slow, manoeuvres. In the project, we will explore efficient algorithmic methods to perform this task based on search algorithms. Additional details can be found here.

Towards Understanding Domain Coherence

Supervisor(s):Prof. Oren Salzman

Requirements:Advanced topics in robotics (236610) / Introduction to Robotics (236927 or 046212)

Informally speaking, domain coherence is the property that a domain contains either ``similar'' problems or ``similar'' robots (or both). Consequently, domain coherence implies that given a motion-planning problem and two ``similar'' robots (for example, two manipulators with roughly the same link lengths, payload, joint limitations, etc.), then a solution obtained for the first robot is ``similar'' to a solution obtained for the second robot. Surprisingly, this intuitive notion is quite challenging to formalize. In this project we will take a data-driven approach to formalizing this notion and demonstrate its usefulness in motion-planning problems.

Resilient motion planning

Supervisor(s):Prof. Oren Salzman

Requirements:Advanced topics in robotics (236610) / Introduction to Robotics (236927 or 046212)

In this project we will investigate the problem of resilient motion planning. Here, we are interested in computing a path that can still be executed even if one of the robot's system's fails. Specifically, we will look at robot manipulators which often have some redundancy built in. For example, to reach any point in space, we are required to have a six degree of freedom (DOF) arm. However, many manipulators are endowed with seven DOFs. This extra flexibility allows a planner to choose between many options when attempting to connect two points. Typically, one option is chosen and the rest are discarded. In this project we will investigate how this redundancy can be used in a systematic way in order to achieve a resilient motion planner. Additional details can be found here.